- Bias and Variance
- bias : 예측값과 실제 정답과의 차이의 평균 (예측값이 정답에서 얼만큼 떨어져 있는가)
- varaince : 얼만큼 예측값이 퍼져서 다양하게 출력될 수 있는가
→ bias & variance는 모델의 복잡도와 관련이 있고, 서로 trade-off 관계


출처1 : https://gaussian37.github.io/machine-learning-concept-bias_and_variance/
출처2 : https://www.pico.net/kb/overfitting-variance-bias-and-model-complexity-in-machine-learning/
- Ensemble
- 앙상블 : 편향 및 분산(오버피팅)을 극복하여 더욱 일반화 된 모델을 만드는 것
| bagging | boosting |
| (서로 다른 sub sample에 대해) 여러 개의 트리 모델 학습 후, 각 트리의 예측을 voting 등으로 조합 |
(서로 다른 sub sample에 대해) 하나의 트리를 업데이트해가면서 학습 |
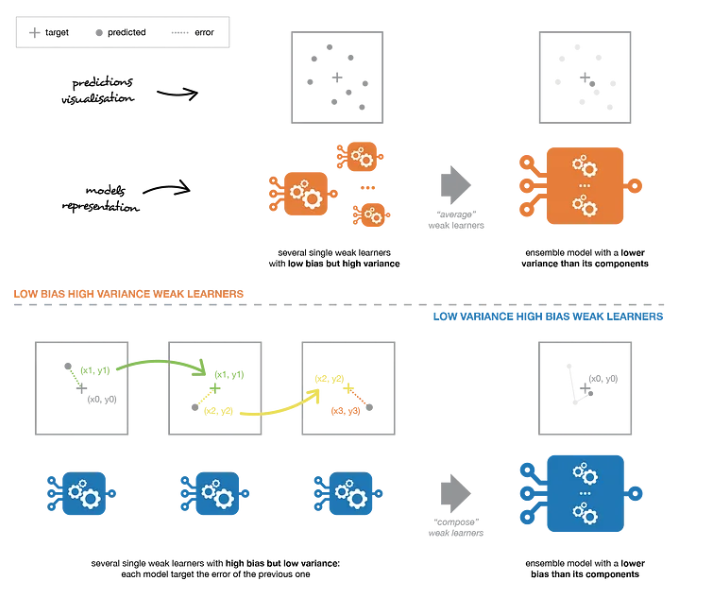
| low bias & high variance (weak learners) - high variance = overfitting = 모델의 복잡도가 높음 - 개별 weak learner들은 모델의 복잡도가 높음 → 각 트리를 앙상블하면서 편향을 손해보는 대신 분산을 줄임 |
high bias & low variance - high bias = underfitting = 모델의 복잡도가 낮음 → 편향을 줄여나가는 방향으로 학습 |
| Random Forest, Extra Trees | Gradient Boosting, XGBoost |
| XGBoost는 gradient boosting 기반(가중치 업데이트)이기 때문에 불균형 데이터 세트에 좋다. - bias를 줄이기 때문에 imbalanced data에 좋음 이러한 이유로 부스팅은 노이즈 변수, oulier 데이터에서는 좋지 않다. |
https://www.educba.com/random-forest-vs-gradient-boosting/ |
| 랜덤 포레스트는 각 weak learner가 독립적이므로 트리 수(estimator)가 많아져도 과적합의 위험이 없지만 부스팅은 이전 weak learner가 업데이트 되면서 트리가 추가되므로 과적합의 위험이 있다. | https://datascience.stackexchange.com/questions/17364/gradient-boosting-tree-the-more-variable-the-better |
| also overfitting does not occur in the random forest but occurs in gradient boosting algorithms due to the addition of several new trees. | https://www.educba.com/random-forest-vs-gradient-boosting/ |
| gradient boosting의 손실함수(=classification에서 log_loss)를 최소화하는 방향으로 sequential하게 업데이트하는 학습 방식으로 인해 bias를 줄일 수 있지만 과적합의 위험이 있다. | https://3months.tistory.com/368 |
| Data 수에 비해 feature 수가 많은 데이터의 경우, 과적합의 위험이 크므로 variance를 줄이는데 집중하는 bagging 방식인 random forest를 사용?? - random forest : independent trees, reduce variance, reduces the likelihood of overfitting
|
https://spark.apache.org/docs/1.6.0/mllib-ensembles.html |
| → 그러나 일반화 성능을 위한 여러 hyper-parameter가 있기 때문에 대부분 성능 좋게 나옴 (ex. n_estimaor, 학습에 사용할 feature 개수, drop out, early stopping, L1, L2 등..) |
|
- overfitting 방지 방법
1. regularization
- L1 norm, L2 norm과 같은 일반화 방법
2. large training set
- 학습 데이터가 많을수록 모집단 분포에 가깝기 때문에 일반화 성능 증가
3. 모델 복잡도 줄임
- feature 개수를 줄임
- 충분하지 않은 데이터에 변수가 많아지면 모델 복잡성이 증가하고 오버피팅 초래 (차원의 저주)
→ feature selection
'Data science > AI' 카테고리의 다른 글
| micro average F1-score와 accuracy가 같은 이유 (0) | 2023.06.16 |
|---|---|
| SHAP (SHapley Additive exPlanations) (0) | 2023.06.16 |
| 공부해야 될 모델 리스트 (0) | 2023.06.16 |
| 이미지 노이즈 종류 및 제거(Image Denoising)/ Gaussian, Median, Bilateral, NLmeans (0) | 2023.04.08 |